形式语言
形式语言和自动机理论中的语言是一个宽泛的概念(不同于传统语言)。
- 一个字母表上的语言就是该字母表的任意字符串的集合。
- 语言中的字符串称为该语言的句子
一个语言应该有两方面来决定:
产生语言的角度(形式语言)
根据语言中基本句子和其他句子的形成规则,产生该语言所包含的所有句子。
接收/识别语言的角度(自动机)
使用自动机模型来接收字符串,接收的所有字符串,也形成一个语言。
定义
语言的定义
对于字母表 ,则 上任意一个子集都其中一种语言。称为 上的一种语言 。
对于 ,,则 是语言 上的句子。
由 文法 产生 语言,从开始符号 出发,经过推导生成句子,由句子组成语言。
一个语言表达的模式是固定的,表示一系列具有某种含义的句子,所以所有句子都是 ,且 都是由 产生。
文法的定义
其中, 表示终结符, 表示非终结符, 表示初始状态, 表示产生式的集合
区分文法和语言:文法是产生语言的规则式子(产生式),语言是一系列文法表达的含义(语义)。
文法(语言)类型
短语结构文法(PSG)
任何文法都是 PSG,0 型文法
上下文相关文法(CSG)
对于 ,都有 成立,则为 1 型文法。
标准形式为:
info
意思为文法是需要依赖上下文 和 的,需要上下文作为条件来产生句子。
上下文无关文法(CFG)
对于 ,都有 且 ,则为 2 型文法。
所有非终结符均出现在产生式左边,且每条产生式只有一个非终结符。
info
意思为和上下文无关,即不需要上下文的帮助也可以产生语言。
右线性文法(RG)
对于 ,都有 或 ,则为 3 型文法。
即左边只能出现一个字母,产生式右侧的非终结符出现在最右边。
文法类型判断
- 任何文法都是 PSG
- 所有产生式 左边长度 右边长度,则为 CSG
- 满足 2 的前提下,产生式左边只有一个非终结符,则为 CFG
- 满足 3 的前提下,产生式右边最多只有一个非终结符,且该终结符只出现在最右边,则为 RG
danger
请注意:CSG,CFG,RG,不含有 (),但开始符号 不出现在产生式右边,则可加入 ,类型不变。
一些例题:

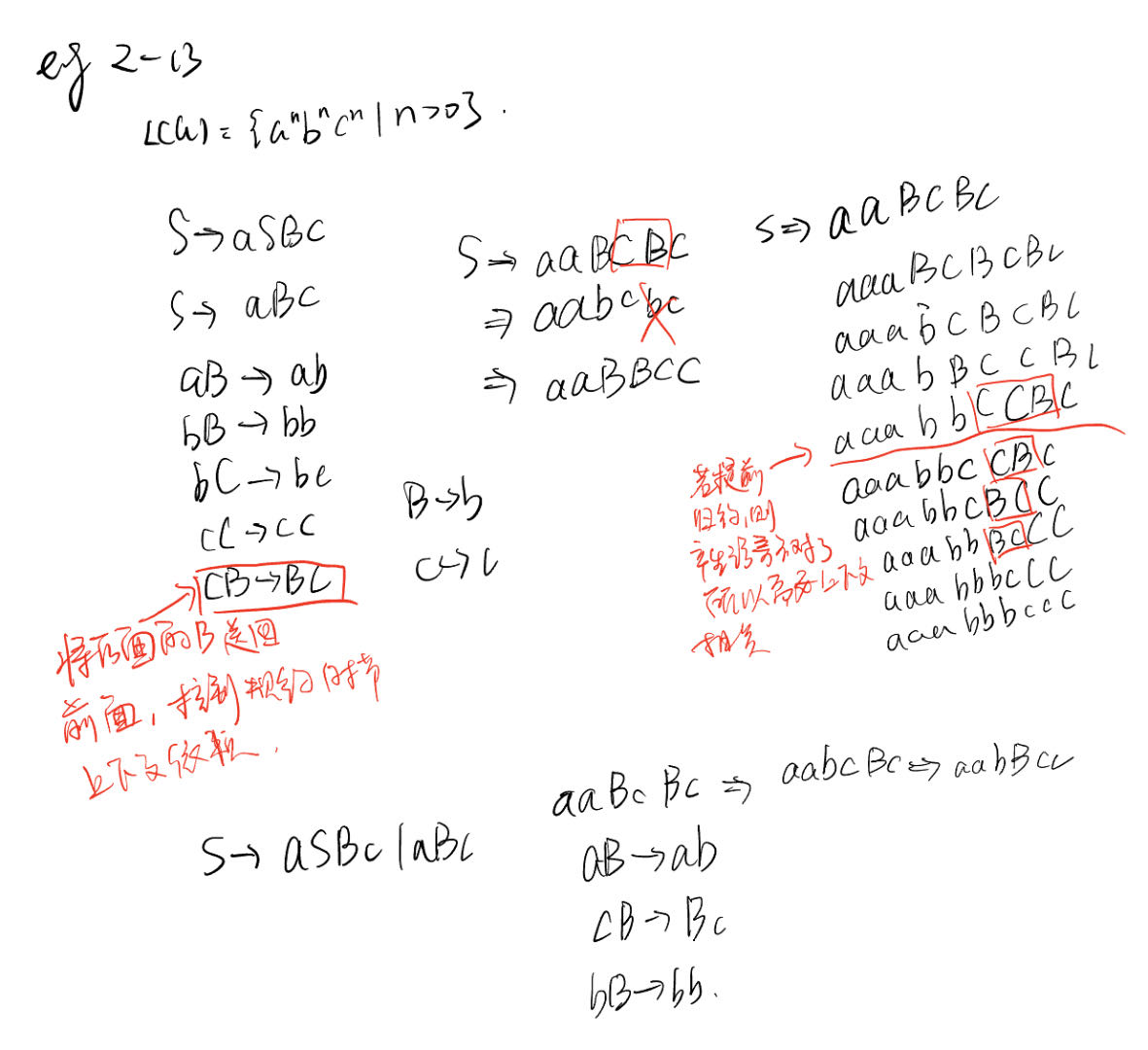

正则表达式


本章核心
如何根据语言表达写出对应的文法。