词法分析
FA 有限自动机
表达状态转换的过程,用来控制状态转化,表示从当前状态下满足什么条件之后应该转向什么状态。分别有 、、、最小化
正规式
符号表示
- | 表示 “或”,表示选择
- * 表示闭包运算,任意有限次的自重复连接
- 表示 “连接”,可省略,连接两个式子
运算优先级
- * 一元运算符优先级最高,左结合
- 其次为 “连接” 运算,左结合
- “选择” | 优先级最低,左结合
正规式和 FA 的转换
:::danger 注意
- 对于正规式转 FA,在 运算中,不是所有的都可以省略左右两边的空串。
- 转换过程中,可以从优先级低的开始分解,优先级从低到高。
:::
- (闭包运算)转换如下图
- (连接)转换如下图
- (选择/或运算)转换如下图
三种运算的优先级从高到低为:
NFA 确定化(子集构造法)
概念
NFA全称为不确定的有限自动机,也就是从一个状态开始,达到终态的过程中可以选择的状态不唯一,下一状态不唯一导致需要进行试探,如果不是正确的路径还要进行回溯。故对 NFA 进行确定化能够提高状态转换的效率。
求法
根据状态转换图得出状态转换矩阵。
确定初态 a,从初态 a 开始,将初态 a 对应的行写到结果表的第一行。
根据初态 a 所接受的状态,如果出现了跟初态 a 不一样的状态 b,则从这个状态 b 开始,将所有 b 状态包含的元素进行合并,得到状态 b 转移的状态,以此类推。
如:红色箭头为第一个新出现的状态,所以将原来状态转移矩阵中对应的状态 b 中包含的元素对应接受的下一个状态,即 。进行并操作。 其他颜色同理,直到没有出现新的状态。
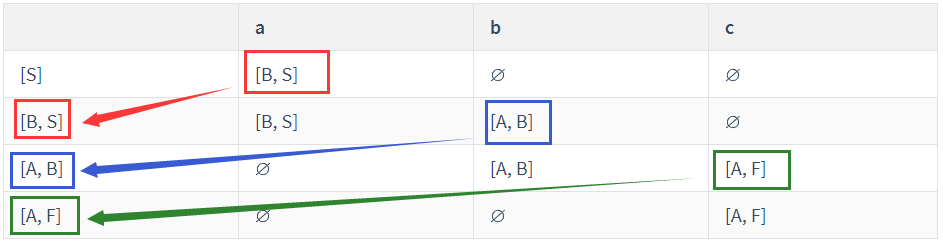
重新命名状态,确定终态,一切包含 NFA 终态元素的集合在确定化后都是终态。
画出 DFA
ε-NFA 确定化(子集构造法)
ε 闭包求解
闭包表示的是所有仅通过标记为 的路径所能够到达的集合,即经过所有带有 标记的路径所经过的点组成的集合。例子如下:
闭包一定包含自己本身,因为任意一个节点都会通过自己回到自己。即
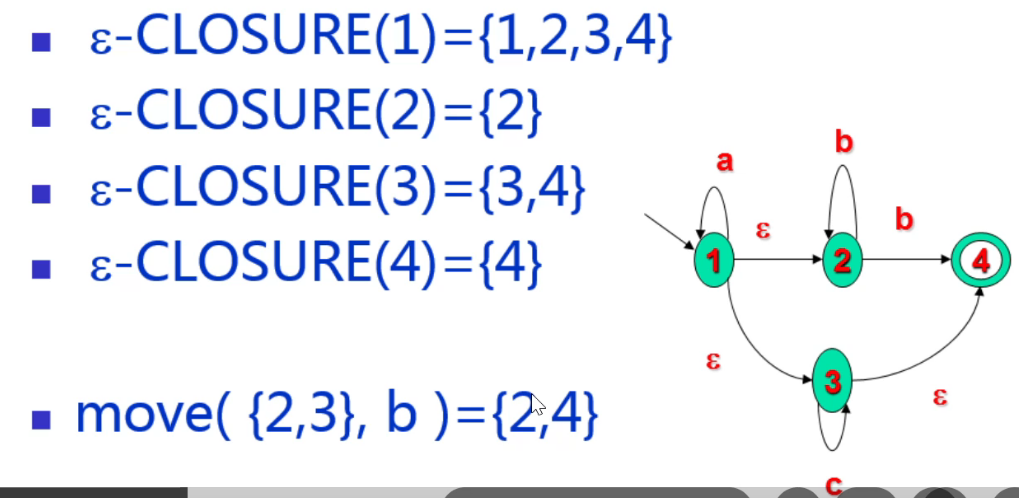
上例中解释如下:
- :1 能通过 、 两条路径到达对应的点,所以它的闭包就包括了 2,3,4。
- :2 没有标记 ε 的路径,所以只有它本身。
- 以此类推.......
求法
根据状态转换图得出状态转换矩阵。
求解状态转换图中所有节点对应的 ε 闭包。
确定初态,从初态 a 的闭包开始,将初态 a 的闭包对应的行写到结果表的第一行,将初态 a 的闭包中包含的元素对应接受的下一状态。
右侧需要填写对 S 计算闭包之后所包含的状态,把当前所包含的状态对应接受的下一个状态全部进行并操作。
将 S,U,R 三个状态对应的下一个状态并起来,得到新的状态。
根据初态 a 所接受的状态,如果出现了跟初态 a 不一样的状态 b,则从这个状态 b 的闭包开始(即)开始,将所有 b 状态的闭包所包含的元素进行合并,得到状态 b 转移的状态,每一步得出结果后要套上 ,用闭包的结果代替。如果 为集合则分别求解后进行并操作,以此类推。
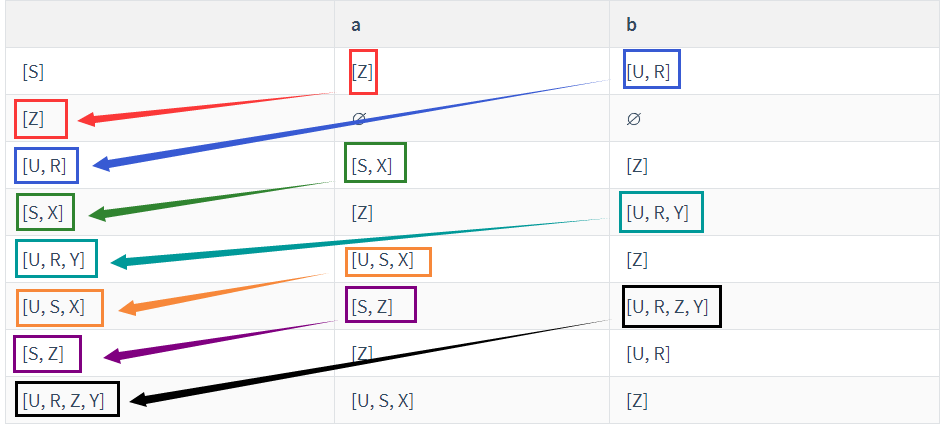
重新命名状态,确定终态,一切包含 NFA 终态元素的集合在确定化后都是终态。
画出 DFA
DFA 最小化
进行最小化要对当前确定化的 FA 进行划分。
划分出终态集和非终态集。
看两个集合的划分,以 为例。
- 对于 而言,,,故无法区分。(说明是等价的)
- 对于 而言,只有一个元素,所以也无法区分。
如果出现可以划分的则对其重新划分后再次判断是否可以继续划分,直到无法划分为止,即:
- 对于 而言,,,。故 不可划分,但 ,不是一家所以可以划分。
修改原 DFA,画出新的状态转换图。