语法分析
文法
正规式描述能力不够,能够定义一些简单的语言,表示给定结构的固定次数的重复或者灭有指定次数的重复,不能描述成对,配对或者嵌套的串,所以才有文法。
句型、句子、语言
单词:满足一定规则的字符串。
句子:满足一定规则的单词序列。
语言:满足一定规则的句子集合。
推导和分析树
推导
推导是指通过使用给定的文法推导出目标的句子,如下例中的 id * id + id。

推导主要有两种,分别如下:
- 最左推导:优先从左往右进行替换。
- 最右推导(规范推导):优先从右往左进行替换。

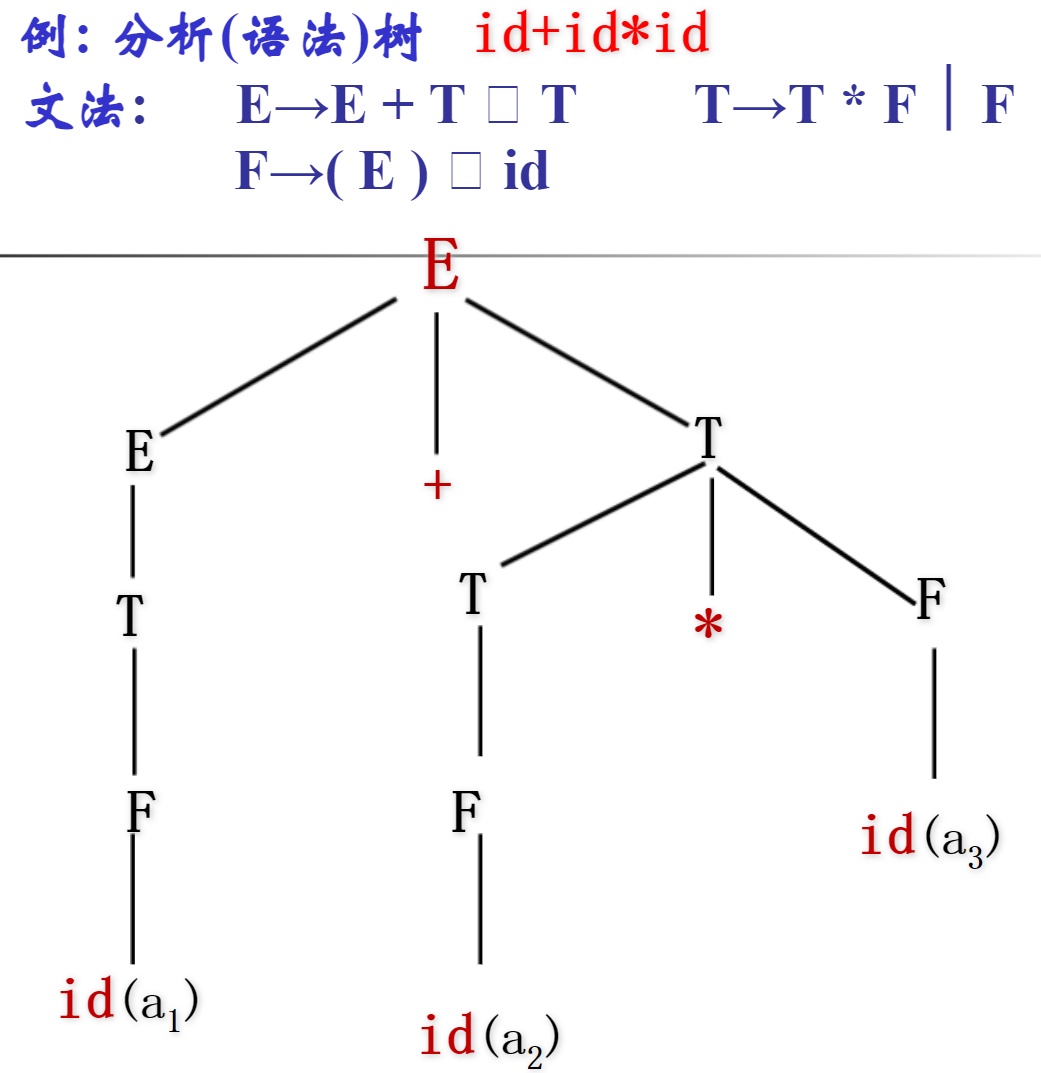
分析树
用树的形式表示句子的语法结构。
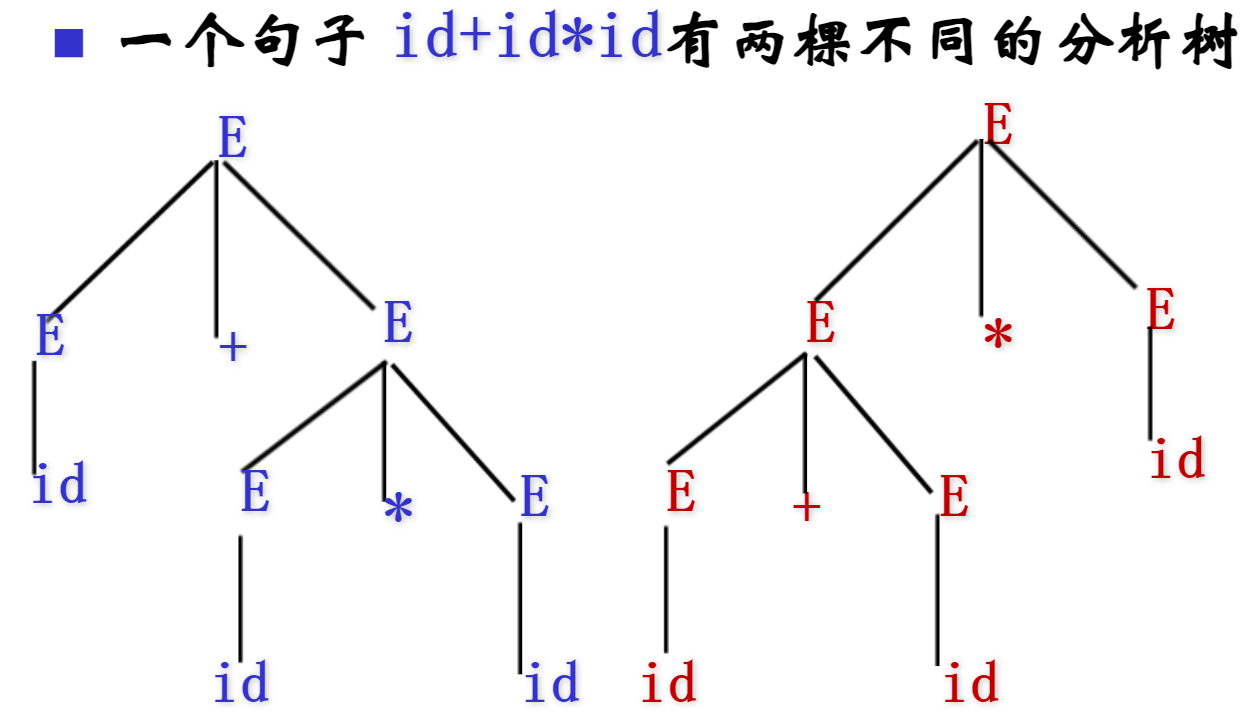
文法的二义性
对于文法来说,有可能会产生二义性,也就是对于一个句型来说,同一个句型能够产生两棵不同的分析树。如下图:
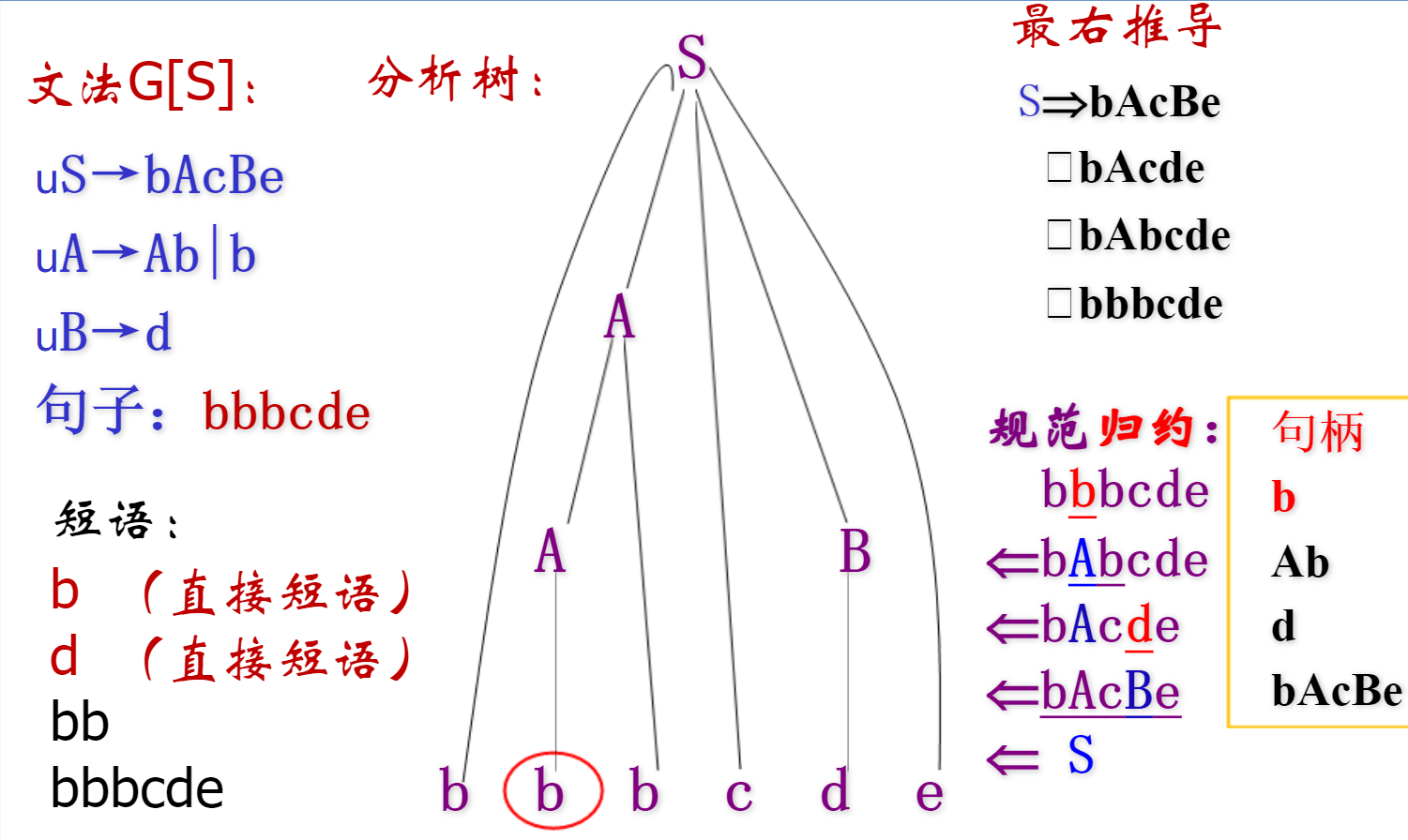
句柄、短语
- 句柄:最左直接短语,就是分析树中的叶子。
- 短语:句子里面的其中一个式子。语法树中子树相对于根的短语。也就是一棵子树的叶子。
自上而下的文法
递归文法
消除递归记得补充上空串,在包含有递归的式子后。

消除左递归的方法:

蓝色框:递归重复的部分。
绿色框:递归的入口。
引入一个额外的字母 ,分解成两条式子转换为右递归。将左边对应颜色部分进行对应即可。
消除间接左递归:
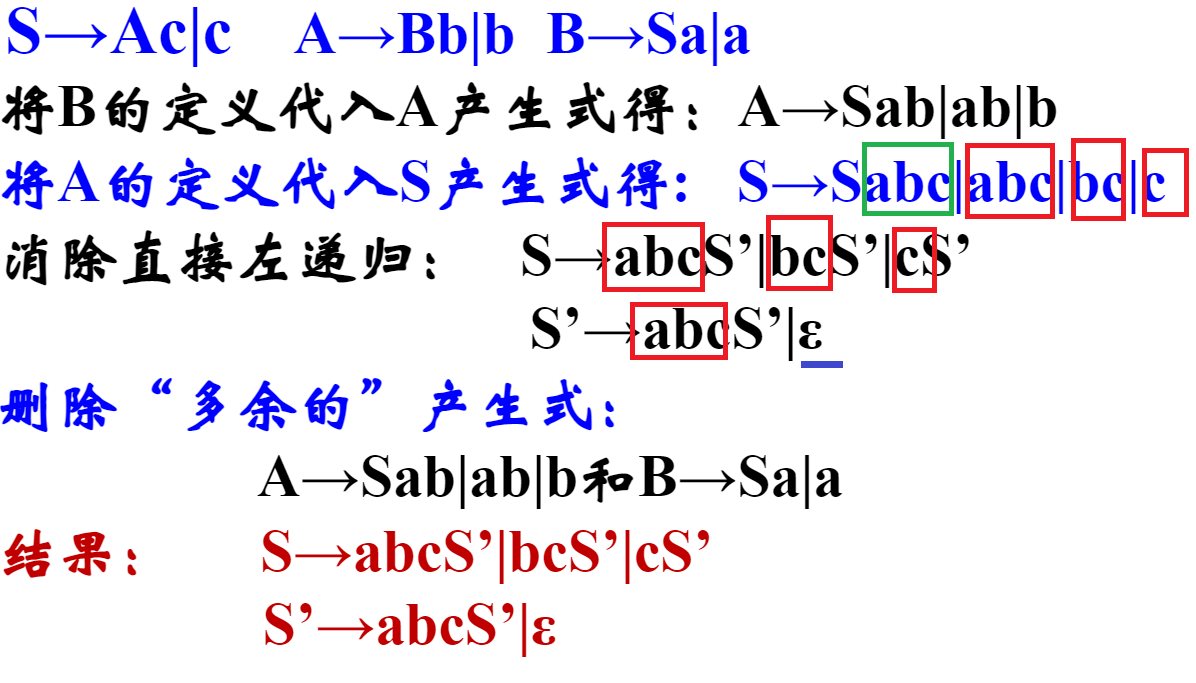
红色框:递归入口的部分。
绿色框:递归重复的部分。
同样引入额外的字母,将带有方框的蓝色式子的颜色方框一一对应。
求解 First 集和 Follow 集
First 集
对于首符号为终结符
对于一个产生式 ,有:
First 集为 ,只关注产生式产生的式子的首个符号,称为首符号集。
tip可能会存在 的情况,则需要把所有的情况考虑,故 First 集为:
对于首符号为非终结符
对于一个产生式 ,有:
- 若 ,则 ,即当首符号为同时要求解
- 否则,,这个过程是多次迭代的,直到找到终结符。
Follow 集
- 将 $ 加入到 ,其中 是文法开始的符号。
- 若 ,则 ,即求 Follow 集只需要看产生式右侧所求符号的后继,将后继符号的 First 集加入到 Follow 集。
- 若 或 ,,即若产生式右侧所求符号的后继为空,则求其产生式左侧符号的 Follow 集。
LL(1)
消除左递归、左公因子。
求每个候选式的 First 集和所有变量的 Follow 集
检查是否为 LL(1) 文法
- 任意两个产生式 满足两个条件(只要看有或的产生式即可):
- 如果 ,那么则看
- 任意两个产生式 满足两个条件(只要看有或的产生式即可):
构造 LL(1) 分析表
表格式为:
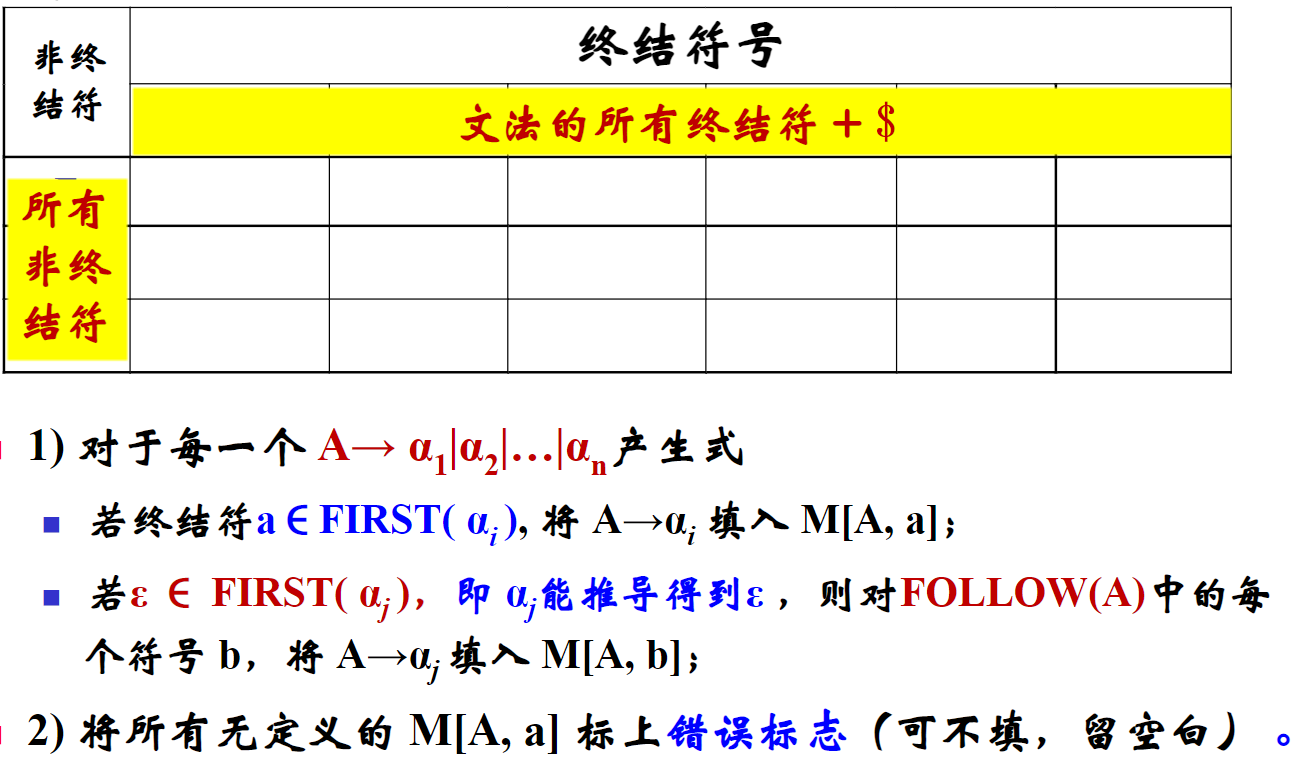
对候选式 的右侧求其 First 集,即 ,最后将 First 集中包含的元素按终结符的列填入到 对应的行,填入元素为 。
如果 的 First 集中包含空串,则 中包含的元素也填入到 对应的行,填入元素为 。
分析句子
- 根据所给句子,从开始符出发(分析栈栈顶),从左往右开始,按照句子的符号在分析表中找对应的列,使用对应的语句。
- 用产生式右部替换分析栈栈顶(产生式右部的式子从右往左入栈)。
- 继续看栈顶查表使用对应的语句。
- 直到分析栈为空结束。


自下而上的文法
构造活前缀 DFA
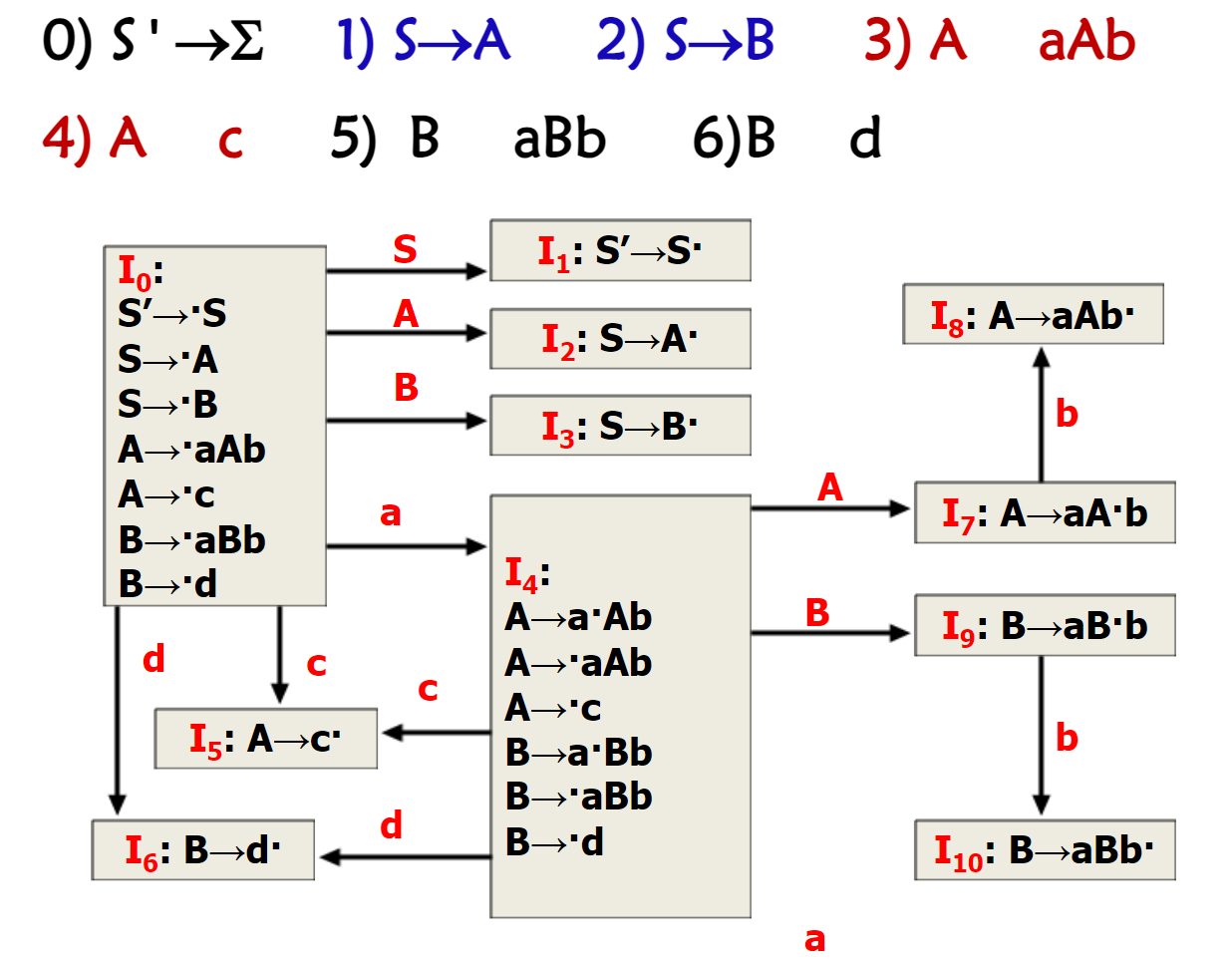
LR(0)
增广文法,添加产生式 。
构造活前缀 DFA。
判断是否为 LR(0) 文法。
构造 LR(0) 分析表。
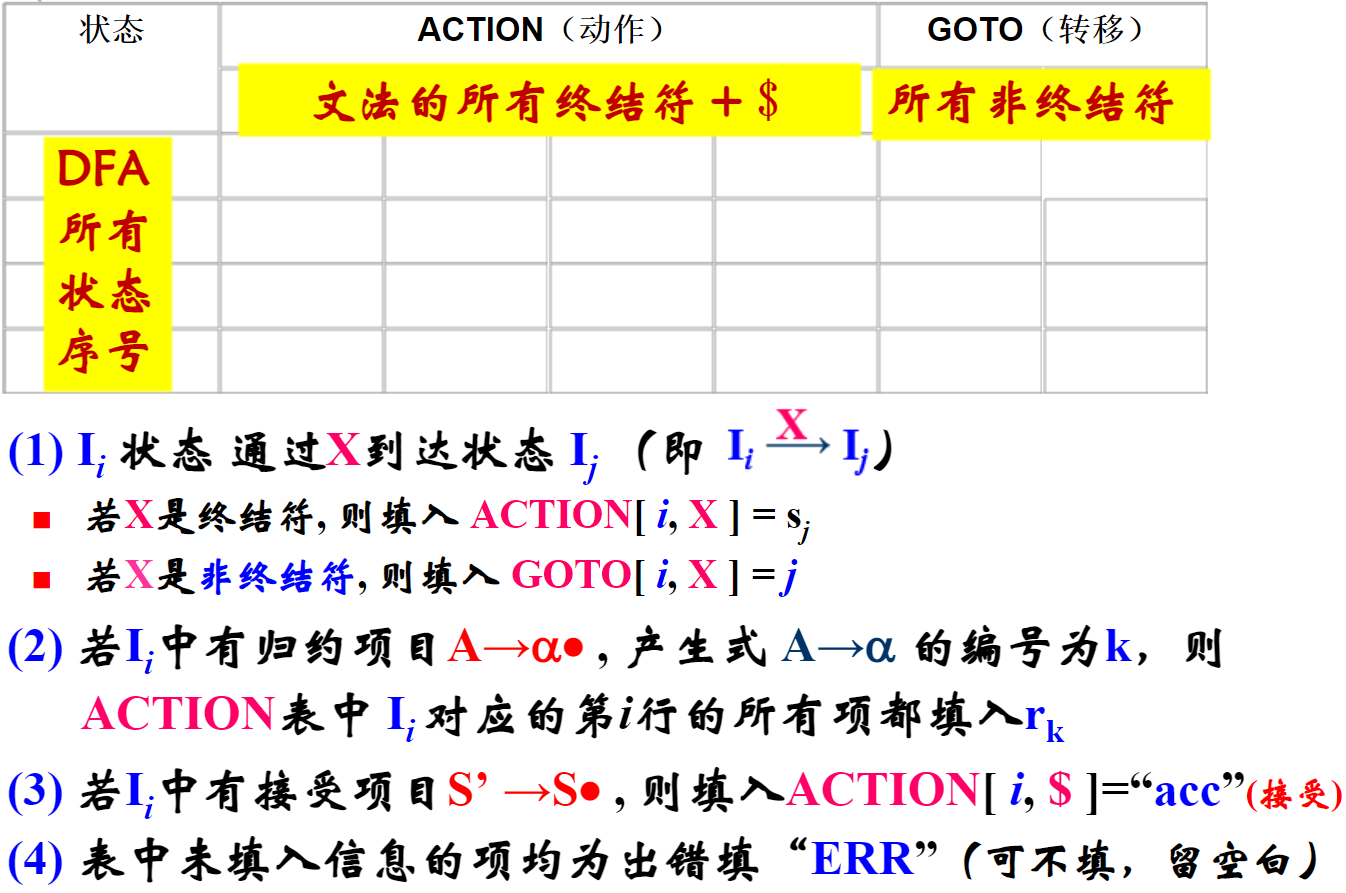
基于分析表分析给定句子。
SLR(1)
增广文法,添加产生式 。
构造活前缀 DFA。
判断是否为 SLR(1) 文法。
构造 SLR(1) 分析表。(考虑 Follow 集)

基于分析表分析给定句子。
LR(1)
增广文法,添加产生式 。
构造活前缀 DFA。(加入第二分量)
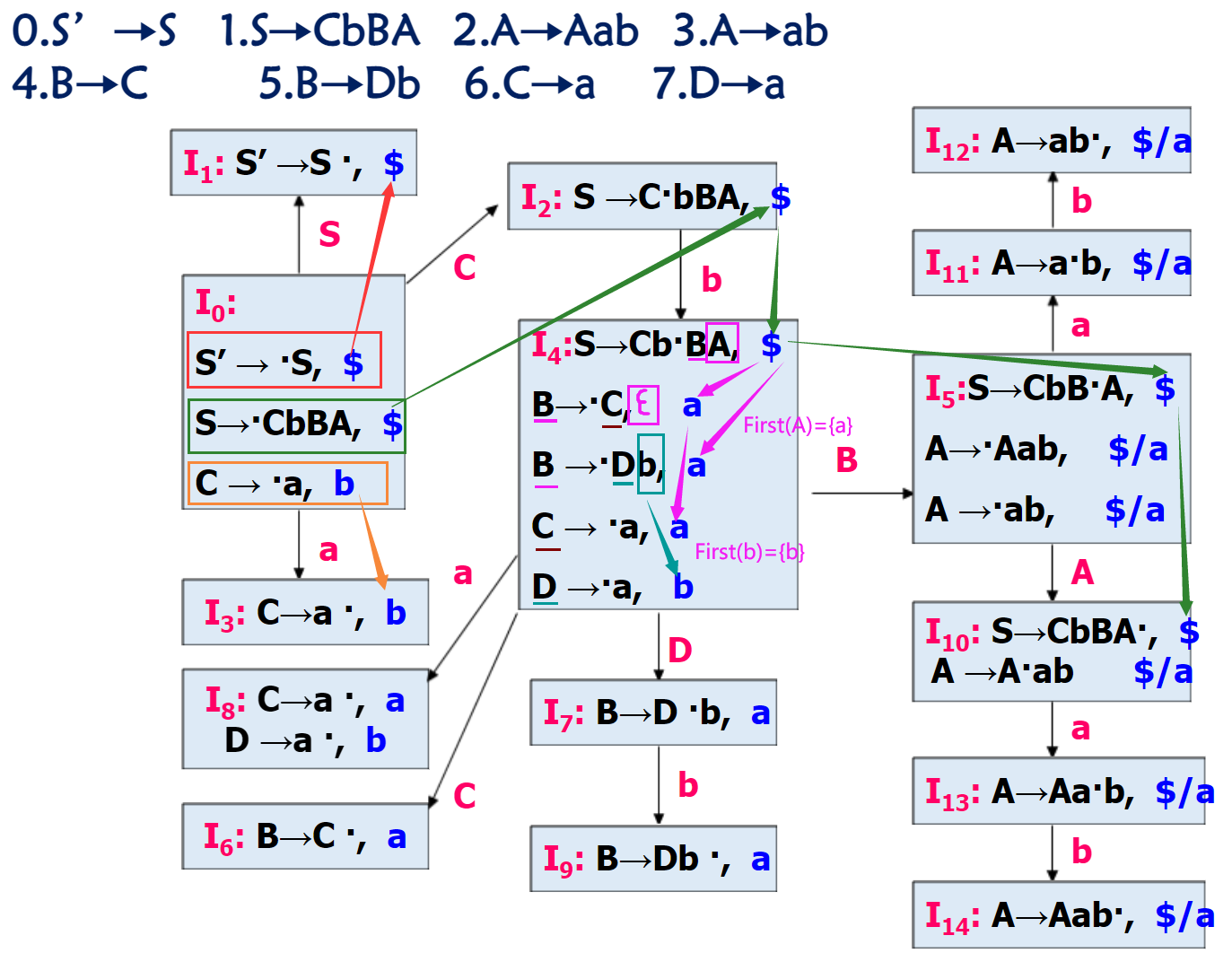
判断是否为 LR(1) 文法。
构造 LR(1) 分析表。(考虑第二分量)
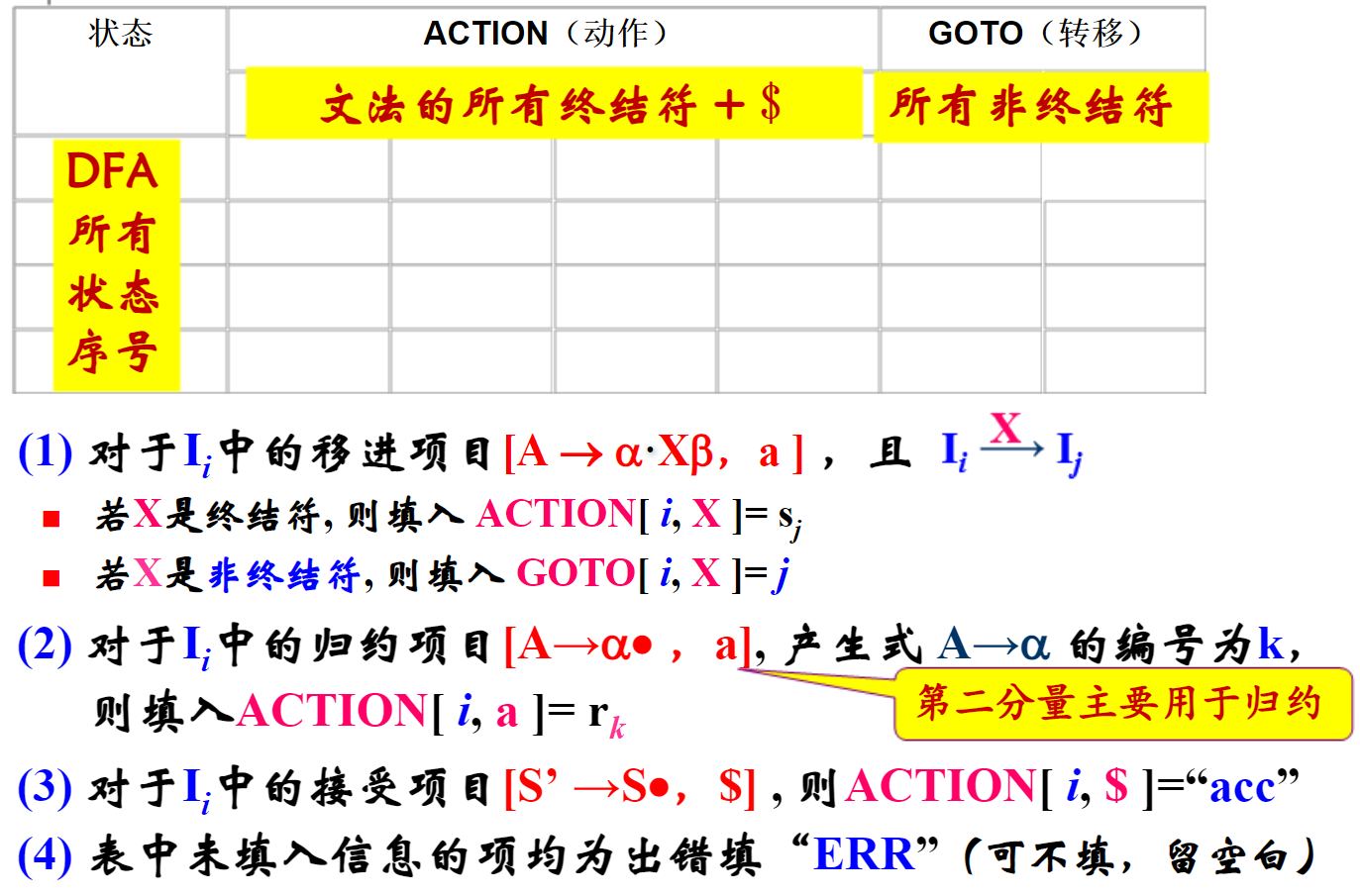
基于分析表分析给定句子。